
Мазмуну:
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 10:36.
- Акыркы өзгөртүү 2025-01-23 14:51.


Тартылган сигналдан жыштыкты өлчөө татаал иш болушу мүмкүн, айрыкча Arduinoдо, анткени ал эсептөө күчү төмөн. Нөлдүк өтүүнү кармоо үчүн жеткиликтүү ыкмалар бар, бул жерде жыштык белгиленген убакыт ичинде канча жолу нөл сызыктан өткөнү текшерилет. Мындай ыкма сигнал ар кандай жыштыктардын айкалышы болгондо иштебеши мүмкүн.
Эгерде сиз мындай фондон болбогон болсоңуз, анда аны коддоо кыйын. Бирок бул кодер музыкага, сигналды талдоого байланыштуу ар кандай долбоорлор үчүн абдан пайдалуу болушу мүмкүн. Бул долбоордун мотиви, анын фонуна кирбестен, Arduinoдо ишке ашыруу оңой болгон кодду даярдоо болчу.
Бул долбоор ФФТнын ишин түшүндүрбөйт, бирок FFT функциясынын колдонулушун түшүндүрөт. Ушул эле процесс тиркелген видеодо да түшүндүрүлгөн.
Эгерде сиз коддун түшүндүрмөсүнө эмес, колдонулушуна гана кызыксаңыз. Сиз 3 -кадамга түз эле өтүп кетсеңиз болот.
1 -кадам: Frequency Transformго киришүү


Ар кандай сигнал ар кандай синусоидалык толкундардын айкалышынан түзүлүшү мүмкүн. Ошентип, кандайдыр бир убакытка негизделген сигналды ар кандай амплитудалардын ар кандай синусунун айкалышы катары көрсөтүүгө болот.
Мен мурунку көрсөтмөлөрдүн биринде DFT (дискреттүү Фурье трансформациясы) ишин түшүндүрүүгө аракет кылдым (https://www.instructables.com/id/Arduino-Frequency…). Бул ыкмалар реалдуу убакытта колдонуу үчүн өтө жай. бул дээрлик пайдасыз кылат.
Сүрөттө f2 жана f5 эки жыштыгынын айкалышынан турган сигнал көрсөтүлгөн. Бул сигнал f1ден f5ке чейинки сыноо синус толкундары менен көбөйтүлөт.
Бул математикалык түрдө көрсөтүлүшү мүмкүн -ар кандай жыштыктагы эки гармоникалык маалымат топтомунун көбөйтүлүшү нөлгө жакын болот (маалыматтын көп саны камырдын натыйжасына алып келиши мүмкүн). Биздин учурда, эгерде бул эки көбөйтүү жыштыгы бирдей (же өтө жакын) жыштыкка ээ болсо, көбөйтүүнүн суммасы нөл эмес сан.
Ошентип, эгер биздин сигнал f1ге көбөйтүлсө, көбөйтүүнүн суммасы нөлгө барабар болот (реалдуу колдонуу үчүн нөлгө жакын). ушуга окшош f3, f4 үчүн. Бирок, маани үчүн, f2 жана f5 чыгаруу нөлгө барбайт, бирок калган маанилерден кыйла жогору.
Бул жерде сигнал 5 жыштык менен текшерилет, андыктан сигналды беш жыштыкка көбөйтүү керек. Мындай катуу эсептөө жогорку убакытты талап кылат. N үлгүлөрү үчүн N*N татаал көбөйтүүнү талап кылары математикалык түрдө көрсөтүлгөн.
2 -кадам: Fast Fourier Transform
DFTди тезирээк эсептөө үчүн FFT алгоритмин Жеймс Кули жана Джон Туки иштеп чыгышкан. Бул алгоритм 20 -кылымдын эң маанилүү алгоритмдеринин бири катары да каралат. Бул сигналды так жана жупташкан бөлүккө бөлөт, бул бир катар керектүү эсептөөлөрдү төмөндөтөт. Аны колдонуу менен жалпы керектүү татаал көбөйтүүнү NlogNге чейин кыскартууга болот. бул олуттуу жакшыртуу болуп саналат.
Сиз FFTтин артындагы математиканы деталдуу түшүнүү үчүн кодду жазып жатканда мен айткан шилтемелерге шилтеме кылсаңыз болот:
1.
2.
3.
4.
3 -кадам: Коддун түшүндүрмөсү
1. Fast синус жана косинус:
Эсептөө FFT ар кандай синус жана косинустун маанисин бир нече жолу алат. Arduino орнотулган функциясы жетишерлик тез эмес жана керектүү маанини берүү үчүн жакшы убакыт талап кылынат. Бул кодду кыйла жайыраак кылат (64 үлгү үчүн убакытты эки эсе көбөйтөт). Бул көйгөйгө каршы туруу үчүн 0дөн 90 градуска чейинки синустун мааниси 255тин эсеби катары сакталат. Муну менен номерлерди калкыма катары колдонуунун зарылдыгы жок болот жана биз аны Arduinoдо 1/4 орунду ээлеген байт катары сактай алабыз. Sine_data глобалдык өзгөрмө деп жарыялоо үчүн коддун үстүнө чапташ керек.
Sine_data дан тышкары, f_peaks деп аталган массив глобалдык өзгөрмө катары жарыяланган. FFT функциясын ар бир иштетүүдөн кийин бул массив жаңыртылат. Бул жерде f_peaks [0] эң үстөмдүк кылган жыштык жана андан кийинки маанилер азаюу тартибинде.
байт sine_data [91] = {0, 4, 9, 13, 18, 22, 27, 31, 35, 40, 44, 49, 53, 57, 62, 66, 70, 75, 79, 83, 87, 91, 96, 100, 104, 108, 112, 116, 120, 124, 127, 131, 135, 139, 143, 146, 150, 153, 157, 160, 164, 167, 171, 174, 177, 180, 183, 186, 189, 192, 195, 198, 201, 204, 206, 209, 211, 214, 216, 219, 221, 223, 225, 227, 229, 231, 233, 235, 236, 238, 240, 241, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 253, 254, 254, 254, 255, 255, 255, 255}; float f_peaks [5];
Бизде синустун мааниси 0дөн 90 градуска чейин сакталгандыктан, синустун же косинустун кандайдыр бир мааниси эсептелиши мүмкүн. Төмөндө сандын биринчи туру нөлдүк ондук чекитке чейин сакталат жана сакталган маалыматтан маанини кайтарат. Бул ыкма бир гана сүзүүчү бөлүмгө муктаж. Бул андан ары түздөн -түз синус баалуулуктарын сактоо менен азайтылышы мүмкүн (255 эсе көп эмес). бирок бул Ардуинонун жогорку эс тутумун жейт.
Жогорудагы процедураны колдонуу тактыкты азайтат, бирок ылдамдыгын жакшыртат. 64 упай үчүн 8 мс артыкчылык берет жана 128 упай үчүн 20 мс артыкчылык берет.
4 -кадам: Коддун түшүндүрмөсү: FFT Функциясы
FFT 2, 4, 8, 16, 32, 64 ж. эгер мааниси 2^n болбосо, анда ал баанын төмөнкү жагын алат. Мисалы, эгерде биз 70 үлгүсүн тандап алсак, анда ал биринчи 64 үлгүнү гана карап, калганын калтырат.
Ар дайым 2^n үлгүдөгү өлчөмгө ээ болуу сунушталат. кайсы болушу мүмкүн:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, …
Out_r жана out_im эки сүзгүчтөрү көп эс тутумду талап кылат. үчүн Arduino наносу эс тутумдун жоктугунан 128ден (жана кээ бир учурларда 128ден) жогору үлгүлөр үчүн иштебейт.
кол коюлбаган int маалыматтары [13] = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048};
int a, c1, f, o, x; a = N; үчүн (int i = 0; i <12; i ++) // деңгээлдерди эсептөө {if (data <= a) {o = i;}} int in_ps [data [o] = {}; // ырааттоо үчүн киргизүү float out_r [data [o] = {}; // трансформациянын чыныгы бөлүгү float out_im [data [o] = {}; // трансформациянын элестүү бөлүгү
Андан кийинки агым төмөнкүчө:
1. Код берилген үлгү өлчөмү үчүн бир аз тескери тартипти жаратат (шилтемелер боюнча битти артка кайтаруу боюнча деталдар: 2 -кадам)
2. Киргизилген маалыматтар түзүлгөн буйрукка ылайык, 3. FFT аткарылды
4. Комплекс санынын амплитудасы эсептелген, 5. Чокулар аныкталып, кемүү иретинде тартипке келтирилген
6. жыйынтыктарга f_peaks аркылуу кирүүгө болот.
[башка маалыматтарга жетүү үчүн (эң жогорку жыштыктан тышкары) кодду өзгөртүү керек, ошону менен жергиликтүү өзгөрмөнү кандайдыр бир алдын ала аныкталган глобалдык өзгөрмөгө көчүрүү мүмкүн]
5 -кадам: Кодду текшерүү


Үлгү үч бурчтук толкуну киргизүү катары берилет. бул толкун үчүн тандоо ылдамдыгы 10 Гц жана толкундун жыштыгы 1,25 Гц.
Чийки өндүрүштөн көрүнүп тургандай, баалуулук Scilab тарабынан эсептелген FFT менен дал келет. бирок, бул баалуулуктар так эмес, бирок синус толкуну менен бирдей эмес.
Чыгаруу жыштыгында массивдин жыштыгы 1.25 жана 3.75. так бааны ар бир жолу алуу зарыл эмес. адатта бул сандар жыштык контейнерлери деп аталат. Ошентип, чыгымдын мааниси көрсөтүлгөн урналар ичинде болушу мүмкүн.
Ылдамдык:
Arduino наносу үчүн төмөнкүлөр талап кылынат:
16 упай: 4ms32 упай: 10ms 64 упай: 26ms 128 упай: 53ms
6 -кадам: Жыйынтык
Бул FFT коду реалдуу убакытта колдонмолордо колдонулушу мүмкүн. Эсептөөнү аяктоо үчүн болжол менен 30 мс кетет. Бирок, анын чечилиши бир катар үлгүлөр менен чектелген. Үлгүнүн саны Arduino эс тутуму менен чектелген. Ардуино Мега же башка жогорку аткаруу тактасынын жардамы менен жакшыртса болот.
эгер сизде кандайдыр бир суроолор, сунуштар же оңдоолор болсо, комментарий жазуудан тартынбаңыз.
Жаңыртуу (5.02.21)
Жаңыртуулар: // ----------------------------- FFT Функциясы --------------- ------------------------------- // float FFT (int [in, int N, float Frequency)
N маалыматтын түрү 255 үлгү көлөмүн колдоо үчүн Integer (учурдагы Байт) болуп өзгөрдү. Эгерде үлгү көлөмү <= 128 болсо, маалыматтын байт түрү колдонулушу керек.
Сунушталууда:
Arduino: Frequency Transform (DFT): 6 кадам

Arduino: Frequency Transform (DFT): бул программа ардуинодогу жыштыктагы өзгөрүүлөрдү эсептөө үчүн, параметрлерди көзөмөлдөө менен. бул FFT эмес. FFT - бул DFTди азыраак убакыт менен чечүү үчүн колдонулган алгоритм. FFT кодун бул жерден тапса болот
Fast Hartley Transform Spectral Stethoscope: 22 Steps

Fast Hartley Transform Spectral Stethoscope: Бул көрсөтмөдөн сиз тез хартли трансформациясын колдонуп, спектралдык стетоскоп жасоону үйрөнөсүз. Бул жүрөк жана өпкө үндөрүн элестетүү үчүн колдонулушу мүмкүн
QuickFFT: Arduino үчүн жогорку ылдамдыктагы FFT: 3 кадам

QuickFFT: Arduino үчүн жогорку ылдамдыктагы FFT: Типтүү Arduino оперативдүү жана иштетүү кубаттуулугуна ээ, жана FFT эсептөөчү-интенсивдүү процесс. Көптөгөн реалдуу убакыт тиркемелери үчүн, бир гана максималдуу амплитудага ээ болгон жыштыкты алуу же жыштык чокуларын аныктоо талап кылынат
Көрүү мүмкүнчүлүгү чектелген адамдар үчүн Arduino жана 3D басып чыгаруу үчүн жакшыртылган автобус тажрыйбасы: 7 кадам

Көрүү мүмкүнчүлүгү чектелген адамдар үчүн жакшыртылган автобус тажрыйбасы Arduino жана 3D басып чыгаруу: Көрүүсү начар адамдар үчүн коомдук транспортту кантип жөнөкөйлөтсө болот? көрүүсү начар адамдар. Т
Arduino үчүн 6 баскыч үчүн 1 аналогдук киргизүүнү колдонуңуз: 6 кадам
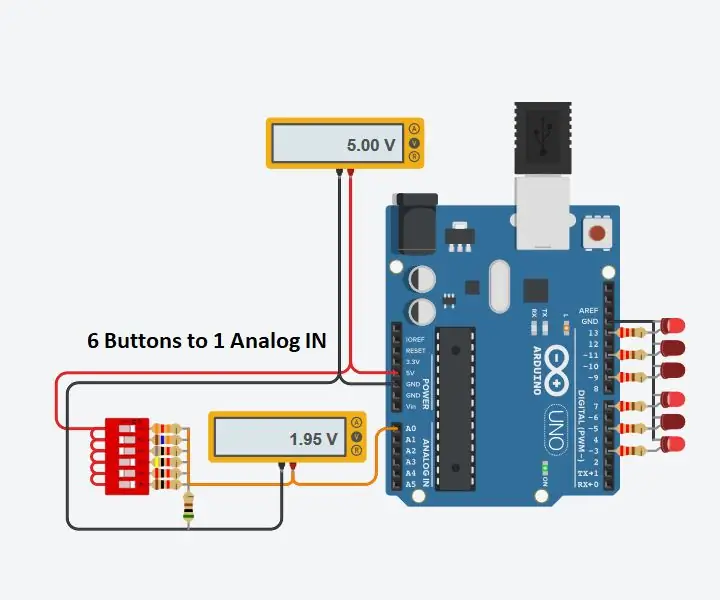
Arduino үчүн 6 баскыч үчүн 1 аналогдук кирүүнү колдонуңуз: Мен Arduino үчүн кантип көбүрөөк санариптик кирүүлөрдү алсам болот деп көп ойлондум. Жакында мен бир нече санариптик кирүүлөрдү киргизүү үчүн аналогдук кирүүлөрдүн бирин колдоно алам деп ойлодум. Мен тез издеп, адамдардын кайда экенин таптым
